Geodetic Evidence that Mercury has a Solid Inner Core
Antonio Genova
The radio tracking measurements of the NASA’s Mercury Surface, Space Environment, Geochemistry, and Ranging (MESSENGER) spacecraft provided crucial information on the interior structure of the planet Mercury. By analyzing the entire radio science (RS) dataset that includes three equatorial flybys and the orbital mission from March 2011 to April 2015, we measured the right ascension (? = 281.0082° ± 0.0009°) and declination (? =61.4164° ± 0.0003°) of the spin pole confirming that Mercury is in the equilibrium Cassini state with an estimated mean obliquity ? = 1.968 ± 0.027 arcmin. This result allowed us to determine the normalized polar moment of inertia C/MR2 of the entire planet by using the method proposed by S. Peale [1] that is based on the assumption that dissipative processes maintain Mercury in the Cassini state. Our measured obliquity yields C/MR2 = 0.333±0.005 that suggests a more differentiated interior structure compared to previous studies [2-3], which assumed larger estimates of C/MR2 (0.346-0.353) recovered from Earth-based radar measurements [4] and MESSENGER altimetric and imaging data [5].
The accurate knowledge of the amplitude of the longitudinal librations through Earth-based radar measurements [4] also enabled the determination of the ratio Ccr+m/C = 0.443±0.019 between the fractional polar moment of inertia of the solid crust plus mantle (Ccr+m) and the polar moment of inertia of the entire planet (C). The dimensionless polar moments of inertia C/MR2 and Ccr+m/C, together with the bulk density of the planet inferred from Mercury’s GM (22031.8636±0.006 x 109 m3 s-2) were used to explore the properties of Mercury’s interior structure, particularly the size of an inner core.
We adopted a Bayesian inversion approach to determine parameters of the internal structure of Mercury, given the three geophysical constraints. A Markov-chain Monte Carlo (MCMC) algorithm [6] was adopted to sample the multi-dimensional parameter space. This method allowed us to determine the probability distributions of the parameters of interest by assuming Gaussian distributions for C/MR2, Ccr+m/C and bulk density that led to the probability function P(j) reported in Eq. 8 of the supplementary information by Genova et al.[7].
The probability distributions of the parameters of interest were explored through random walkers. We used multiple chains starting each parameter with different initial values that were varied randomly. At each stepj, we summed the solution j-1to the step size of each parameter multiplied by a random number from a Gaussian distribution to construct an interior model with values of the three geophysical constraints that were then compared against the observed values. A solution jwas always accepted when the ratio of the probability functions P(j)/ P(j-1)was > 1, and was also accepted if P(j)/ P(j-1) was < 1 but larger than a random number between 0 and 1 generated from a uniform distribution. If the probability distributions ratio was smaller than that random number, the solution j was not accepted and a new solution was tried from the solution j-1. This approach is based on the Metropolis-Hastings algorithm [8-9].
The number of unique chains adopted for each case in our study is 15. Each chain was stopped by using a convergence criterion that was fulfilled when the average values of the geophysical constraints did change less than 1% after 50,000 models [7]. Our chains in general ran for at least 400,000 models each. To compute the final histograms of the parameters, we mixed these unique chains by ruling out the first 30,000-40,000 models in each chain (burn-in) and then selected a model from one of the chains (chosen randomly) by skipping k= 9 models in all chains. For all the interior structure base models, with this downsampling, we ended up on average with between 50,000 and 90,000 models.
The results presented by Genova et al.[7] included five different cases that relied on two different approaches. A four-shell planet modeled with inner core, outer core, mantle, and crust was studied by only assuming that the density (constant within each shell) increases with depth. The other four cases were based on a multilayer approach that consists in dividing each shell of the interior into 1-km-thick sublayers to account for the effects of pressure on density and gravitational acceleration and to solve the equation of state (EoS) in the mantle and the core. These four distinct scenarios considered sulfur (S) or silicon (Si) as the principal light element that is alloyed with iron in the core. The scenario investigated in our study include the following: Fe-S models with a variable percentage of sulfur (0-25%) in the outer core and an inner core of pure iron (Fe-S case), Fe-S models otherwise similar but with a solid Fe3S layer overlying the inner core (Fe3-S case), Fe-Si models with the same weight fraction for Si (0-25%) in both the inner and outer core (Fe-Si case), and models featuring a fluid outer core with two distinct layers of molten Fe-Si and Fe-S alloys and a solid Fe-S layer at the top of the core (Fe-S-Si case).
The internal structure models generated by our MCMC process with these five scenarios provide geodetic evidence that Mercury has a solid inner core with a radius ric between 0.3 and 0.7 that of the outer core roc. Figure 1 shows the histograms of the ratio ric/rocfor the samples of the 4-layer and multilayer Fe-Si case MCMC solutions.
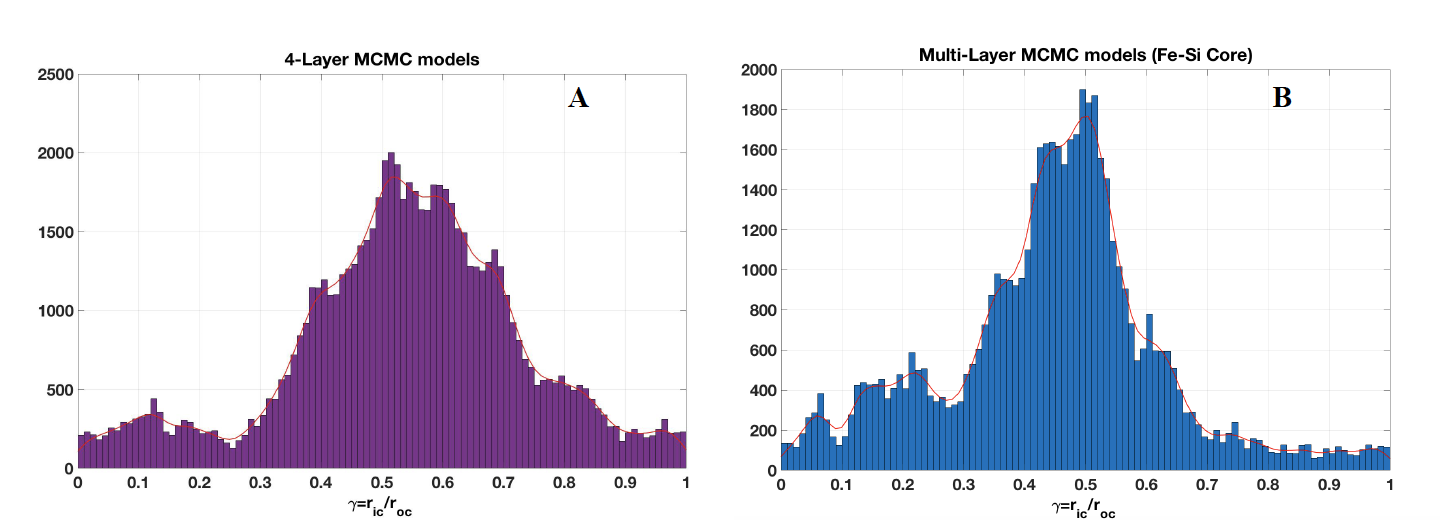
Figure 1. Histogram of the ratio between inner and outer core radii for the samples of 4-layer (A) and multilayer Fe-Si case (B) MCMC solutions.
Data Usage Policy
Our latest estimates of Mercury orientation and gravity solution and the results of the MCMC simulations are presented in the following paper:Genova, A., Goossens, S., Mazarico, E., Lemoine, F. G., Neumann, G. A., Kuang, W., Sabaka, T.J., Hauck, S.A. II, Smith, D. E., Solomon, S.C., & Zuber, M. T. (2019). Geodetic evidence that Mercury has a solid inner core. Geophysical Research Letters, doi:10.1029/2018GL081135
Please cite this manuscript if using the resulting interior models.
Here below we provide the parameters of all the selected MCMC interior models for the five different scenarios described in detail in the supporting information of the manuscript.
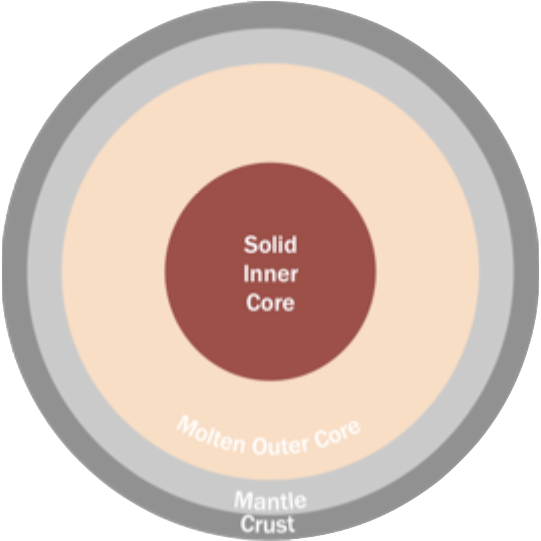 Case 1 [4-layer model] :
MCMC model results
Case 1 [4-layer model] :
MCMC model results
 Case 2 [Fe-Si inner and outer cores] :
MCMC model results
Case 2 [Fe-Si inner and outer cores] :
MCMC model results
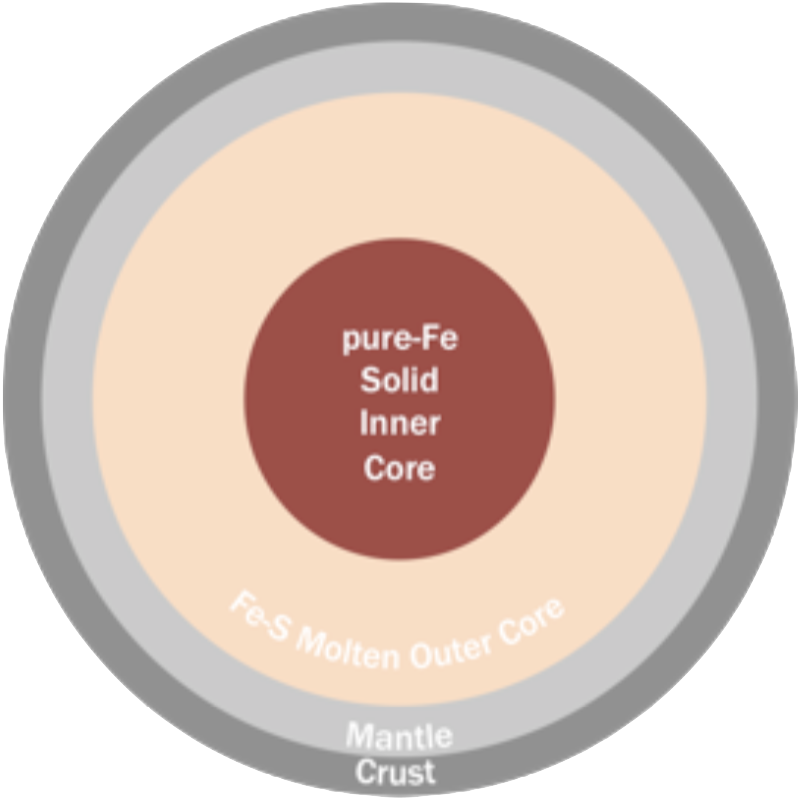 Case 3 [Pure-Fe inner core, Fe-S outer core] :
MCMC model results
Case 3 [Pure-Fe inner core, Fe-S outer core] :
MCMC model results
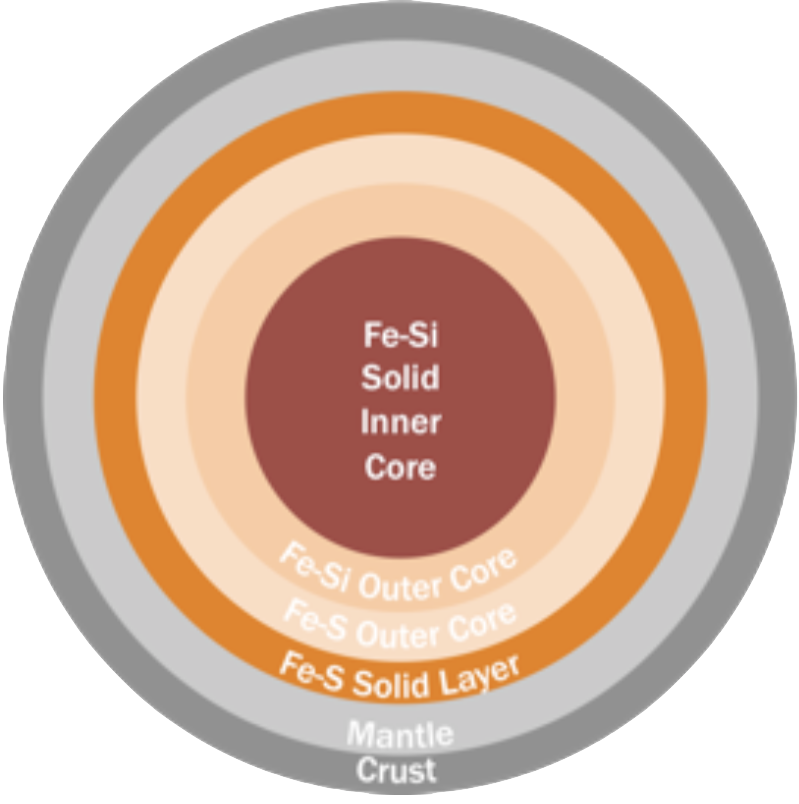 Case 4 [Fe-Si inner core, Fe-Si and Fe-S outer core, Fe-S solid layer] :
MCMC model results
Case 4 [Fe-Si inner core, Fe-Si and Fe-S outer core, Fe-S solid layer] :
MCMC model results
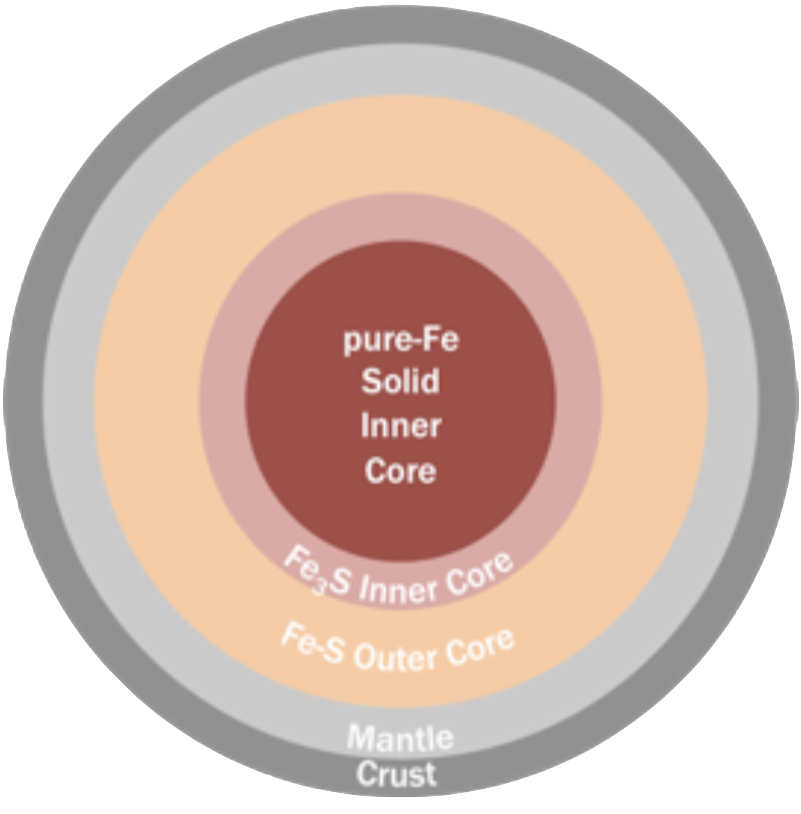 Case 5 [pure-Fe and Fe3S inner core, Fe-S outer core] :
MCMC model results
Case 5 [pure-Fe and Fe3S inner core, Fe-S outer core] :
MCMC model results
References
[1] Peale, S. J., Phillips, R. J., Solomon, S. C., Smith, D. E., & Zuber, M. T. (2002). A procedure for determining the nature of Mercury’s core. Meteorit. Planet. Sci., 37(9), 1269–1283, doi:10.1111/j.1945-5100.2002.tb00895.x.
[2] Hauck, S. A., II, Margot, J.-L., Solomon, S. C., Phillips, R. J., Johnson, C. L., Lemoine, F. G., . . . Zuber, M. T. (2013). The curious case of Mercury’s internal structure. J. Geophys. Res. Planets, 118(6), 1204–1220, doi:10.1002/jgre.20091.
[3] Knibbe, J., & van Westrenen, W. (2015). The interior configuration of planet Mercury constrained by moment of inertia and planetary contraction. J. Geophys. Res. Planets, 120(11), 1904–1923, doi:10.1002/2015JE004908.
[4] Margot, J.-L., Peale, S. J., Solomon, S. C., Hauck, S. A., Ghigo, F. D., Jurgens, R. F., . . . Campbell, D. B. (2012). Mercury’s moment of inertia from spin and gravity data. J. Geophys. Res., 117(E12), E00L09, doi:10.1002/2015GL065152.
[5] Stark, A., Oberst, J., Preusker, F., Peale, S. J., Margot, J.-L., Phillips, R. J., . . . Solomon, S. C. (2015). First MESSENGER orbital observations of Mercury’s librations. Geophys. Res. Lett., 42(19), 7881–7889.
[6] Mosegaard, K., & Tarantola, A. (1995). Monte Carlo sampling of solutions to inverse problems. J. Geophys. Res., 100(B7), 12,431–12,447, doi:10.1029/94JB03097.
[7] Genova, A., Goossens, S., Mazarico, E., Lemoine, F. G., Neumann, G. A., Kuang, W., Sabaka, T.J., Hauck, S.A. II, Smith, D. E., Solomon, S.C., & Zuber, M. T. (2019). Geodetic evidence that Mercury has a solid inner core. Geophysical Research Letters, doi:10.1029/2018GL081135
[8] Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., & Teller, E. (1953). Equation of state calculations by fast computing machines. J. Chem. Phys., 21(6), 1087–1092, doi:10.1063/1.1699114.
[9] Hastings, W. K. (1970). Monte Carlo sampling methods using Markov chains and their ap plications. Biometrika,57(1), 97–109, doi:10.2307/2334940.