NASA’s Planetary Geology, Geophysics and Geochemistry Laboratory

Measuring the Venus Loading Love numbers with VERITAS

The complex dynamics of the Venus atmosphere produces a periodic mass redistribution pattern. Moving atmospheric masses create a time variable modulation of the gravity field of Venus. Said gravity signal depends on the net transport of mass across the globe and on the response of the solid body to the atmosphere loading its crust. The gravitational response to the atmospheric loading, parametrized through the loading Love numbers k_l', depends on the interior structure of the planet, most notably on the viscosity of the mantle. Measuring the loading Love numbers of Venus would provide new and supplementary constraints for its interior structure determination.

he upcoming NASA VERITAS mission to Venus, will be capable of determining the gravity field of the planet to unprecedented level of detail, and will be sensitive to the gravitational contribution of the atmosphere. We have tested the prospect of measuring Venus' loading Love numbers with VERITAS for understanding first if such a measurement is possible, and secondly what would it imply for the efforts of constraining Venus' deep interior structure.


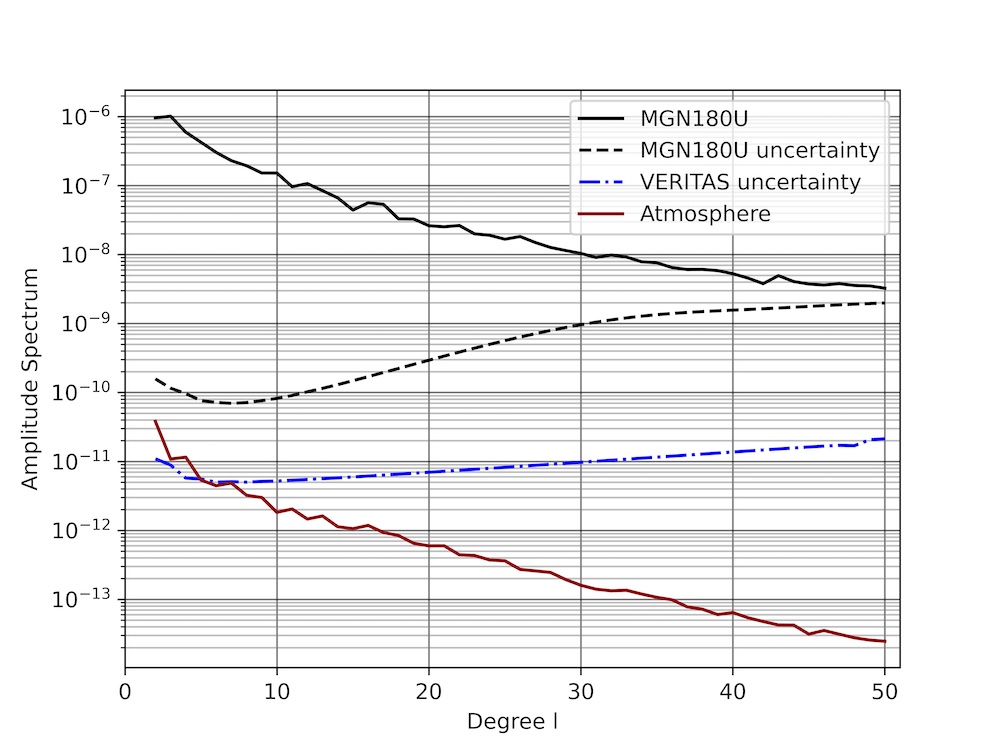
Figure 1. Amplitude spectra of the Venus gravity field measured by Magellan and the associated uncertainty (black solid and dashed lines, respectively), the predicted uncertainty on the gravity field measured by VERITAS (blue dash-dotted line) and the amplitude of the gravity field induced by atmospheric mass redistribution (red line). The lowest degrees of the atmospheric field are above the VERITAS noise floor.


Figure 2. Atmospheric pressure anomalies over one Venus solar day. The pressure field has been obtained from [Garate-lopez et al., 2018].

The first task to be addressed, for answering these questions, consists in understanding the dependence of the Love numbers to the interior structure of Venus. To this aim we have calculated the tidal and loading Love numbers of Venus based on the latest interior models proposed in literature (notably by Dumoulin et al., 2017 and Xiao et al., 2021). These models vary interior density distributions, viscosity profiles, core radius and core status (solid/liquid) allowing us to assess the relation between these quantities and the load Love numbers. The Love numbers have been computed using the TidalPy library which solves the viscoelastic-gravitational problem using the shooting method. The shooting method readily allows for the effects due to compressibility to be explored in a computationally stable way. We have found compressibility to be an important factor for a planet like Venus, especially for the calculation of the loading Love numbers. By computing the Love numbers on such a wide spectrum of interior models we have assessed the expected ranges of values showing a 34% and 22.5% variation in the tidal Love number k₂ and 43.1% and 22.1% in the loading Love number k₂' under the assumption of a liquid and solid core, respectively. We have computed the full set of Love numbers (tidal, loading, and vertical displacement h_l) up to degree 10 for the hundreds of interior model variations considered (see Data section for more details).


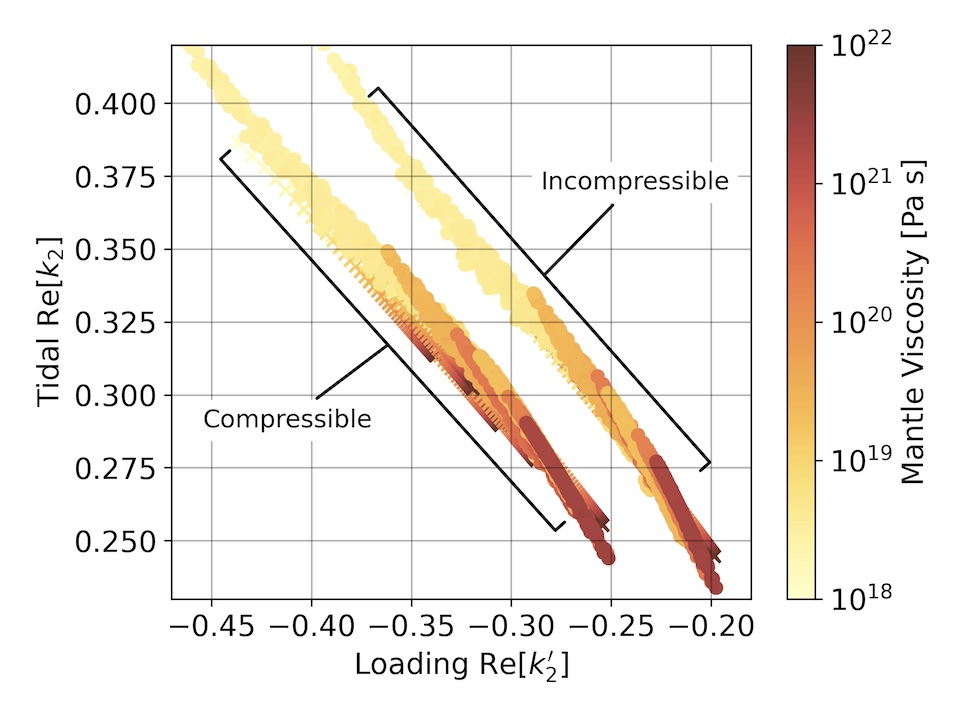
Figure 3. Comparison of the computed tidal and loading Love numbers under the compressible and incompressible assumptions.


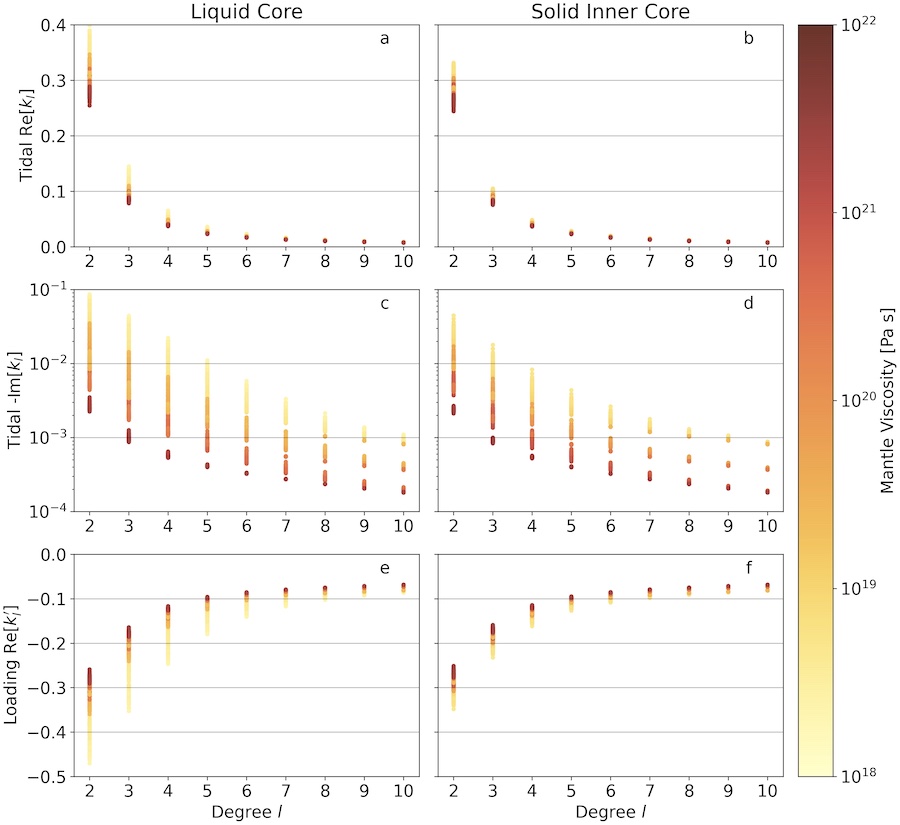
Figure 4. Tidal and loading Love numbers values as a function of the degree, with varying assumptions on the mantle viscosity.

To assess the VERITAS sensitivity to k_l' we have run a set of high-fidelity numerical simulations reproducing the nominal operational scenario of the gravity science experiment. We have focused on understanding the role that systematic errors, arising from uncertain knowledge of the full dynamical environment of the probe, including the planet's static gravity field and the underlying atmospheric model, could have on the final estimate of the Love numbers (more details can be found in Cascioli et al., 2023).

We have shown that VERITAS will be able to measure k₂' to a level of 10%and 4% of the maximum expected range, when considering Doppler tracking data only and Doppler tracking combined with radar tie points, respectively. Depending on the assumptions, moreover, VERITAS will have sensitivity also to k₃' and k₄'.

The simultaneous measurement of k₂ and k₂' define a 3-dimensional measurement in the phase space of Venus Love numbers, namely the real and imaginary portions of the degree-2 tidal Love number at the tidal forcing period of 58.3 days (frequency ω_T), and the real portion of the loading Love number. Since the diurnal thermal tides are the principal contribution to the atmospheric loading, the loading Love numbers are assumed to be measured at the solar forcing period of 116.75 days (frequency ω_S). In concert, these three values (along with other measurements of, e.g., the moment of inertia factor, k₃', k₄') can be used to determine the most likely interior and thermal state of Venus in both a structural and rheological context. In Figure 5, we show how measurements made by VERITAS can narrow the most likely mantle viscosity for the planet. The small observational uncertainties (shown as error bars in the figure) calculated for the real and imaginary tidal Love numbers are small enough for future VERITAS measurements to isolate a small number of likely interior models from those considered by Xiao et al., 2021 and Dumoulin et al., 2017. These two parameters cannot alone capture the entire spectrum of possible models since, as shown in Figure 5, this would correspond to projecting the whole model cloud onto the (Re[k₂], Im[k₂]) plane, losing information from the third dimension provided by the loading Love number. The uncertainty in the loading Love number, although substantially larger, can further constrain the likely composition, viscosity, as well as other rheological parameters.


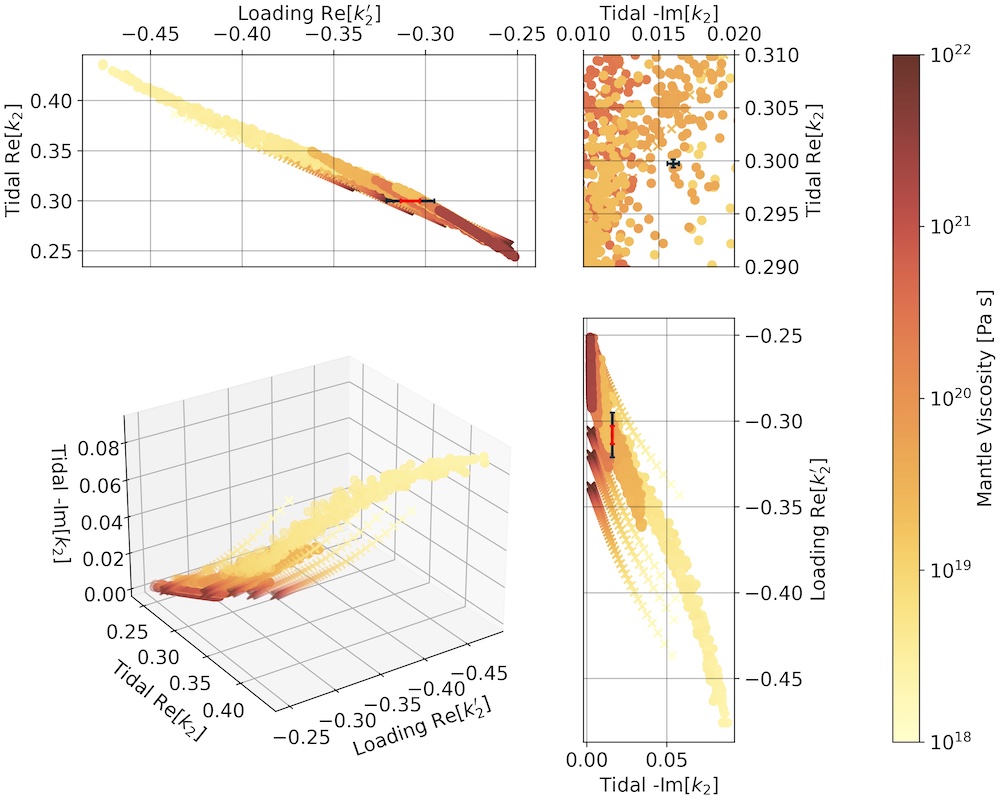
Figure 5. Tidal and loading degree-2 Love numbers as a function of mantle viscosity. Error bars show the VERITAS predicted measurement uncertainty (black: Doppler only, red: Doppler + tie points).

This consideration is particularly true for interior models with low mantle viscosities, where the effects of tidal dissipation become dominant. There exist well-determined relationships between different sets of Love numbers. For example, Saito (1978) gives:
k_l' = k_l - h_l (1)
where h is the vertical displacement tidal Love number, relating the tidal gravitational perturbation to the radial displacement of the surface of the body (for a given degree l). This relation was obtained under the hypothesis of a purely elastic response of the planet. When considering the viscoelastic gravitational problem, this relationship is formally correct only at a given forcing frequency ω:
k_l' (ω) = k_l (ω) - h_l (ω) (2)


Figure 6 shows the graphical representation of this equation. It demonstrates that the elastic relation between Love numbers does not hold, especially for low values of the mantle viscosity. The deviation of the viscoelastic interior model values from the linearity given by the elastic relation, for low viscosity values, makes explicit the importance of an accurate measurement of k₂' as the full spectrum of possible interior models cannot be described with two parameters (linear relation between real and imaginary Love numbers).


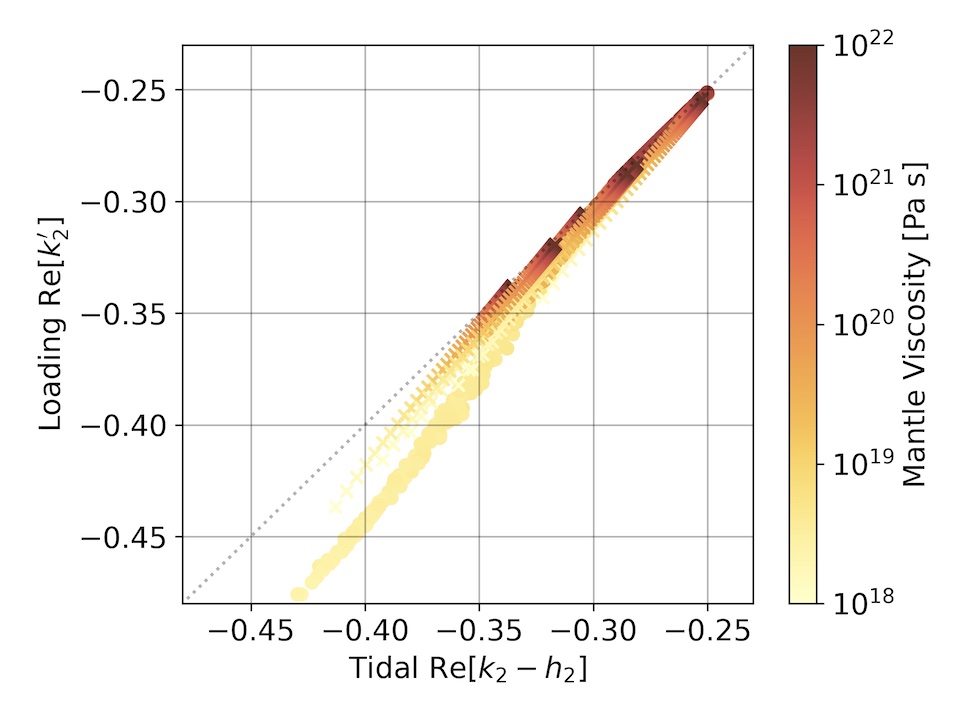
Figure 6. Graphical representation of Equation 2. The diagonal line represents the elastic limit (i.e., Equation 1).


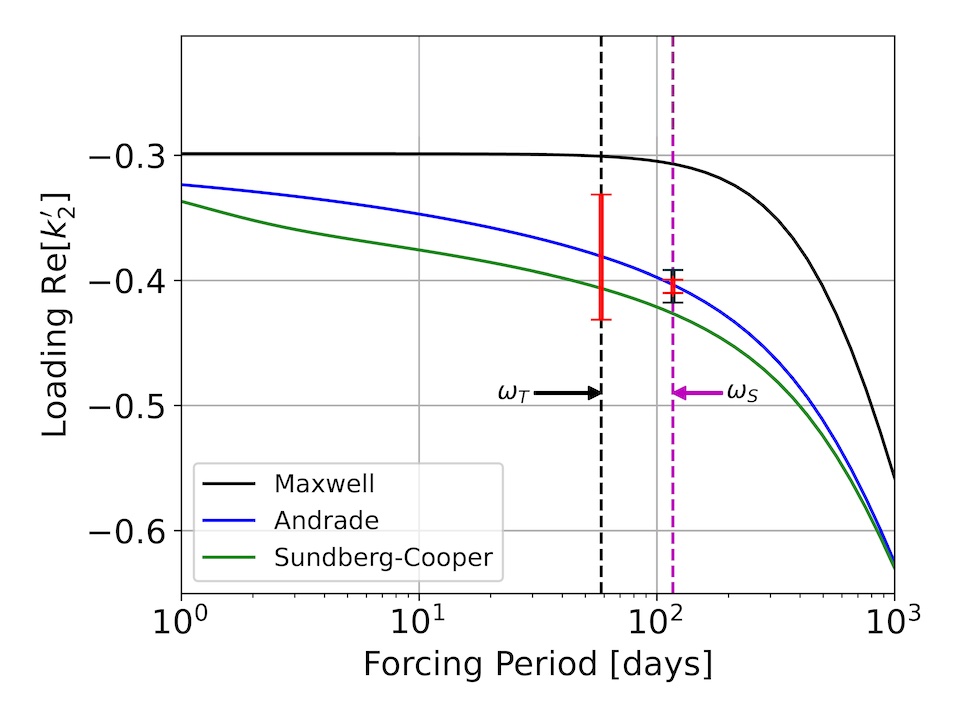
Figure 7. Degree-2 loading Love number amplitudes as a function of the forcing period, for different rheologic laws. Error bars represent the predicted VERITAS measurement capabilities.

As we discussed, VERITAS will measure the loading Love number at the diurnal forcing frequency ω_S. VERITAS will also measure the tidal Love numbers k_2 and h_2 at the tidal (semidiurnal) forcing frequency ω_T (additional details in Cascioli et al., 2021).
This allows to write the relation:
k₂' (ω_T) = k₂ (ω_T) - h₂ (ω_T) (3)

From which the loading love number at the tidal frequency k₂' (ω__T) can be derived. It is important to underline that the measurement of k₂' (ω__T) obtained this way is completely model independent, relying only on the very general assumptions needed to obtain Equation (2). Figure 7 shows how the concurrent measurement of k₂' at the two frequencies ω_T and ω_S has the ability of constraining two points on the amplitude-frequency curve for the loading Love number. We argue that this may help discriminate different rheological laws, and ascertain parameters governing a given rheology. The precise quantification of the constraining power of these measurements, in combination with other key geophysical parameters estimates (such as the MOIF), would require a full inversion of the interior structure model of Venus (e.g., using Monte Carlo Markov Chain techniques). This task goes beyond the scope of this work, and will be part of future focused follow-on investigations.

Data

Data Usage Policy

Product Keywords