NASA’s Planetary Geology, Geophysics and Geochemistry Laboratory

Mars Crust Density from Gravity & Topography

Knowledge of the crust of a planet is important to constrain its formation and evolution. The average bulk density of the crust is an important geophysical parameter, for example in studies of the planet's crustal thickness, its topographic support, and of its thermo-chemical evolution. Yet even with in-situ samples it is difficult to determine, as exemplified by the results of the Gravity Recovery And Interior Laboratory (GRAIL) mission: owing to the combination of high-resolution topography and high-resolution gravity, the bulk crustal density was found to be lower than assumed. For other terrestrial planets, the resolution of the models of the gravity field is often deemed too low to reliably estimate the bulk crustal density. As a consequence, the crustal density is assumed in geophysical studies, and a conservative range (e.g., spanning 2700-3100 kg/m³) is adopted.

We have derived a constraint for use in gravity field determination from satellite tracking data that improves correlations of the gravity field with topography, while a scale factor between the two is determined completely by the data. This makes the constraint, and thus the resulting gravity field model, independent of some model crustal density. The constraint assumes some description of the gravity field model, which we call x_a, and it assigns infinite variance in this x_a direction. It thus has one degree of freedom, and we call our constraint rank-minus-1 (RM1). The constraint is applied with a damping factor λ, and it can be shown that for λ -> ∞, the solution for the gravity field model x will be α x_a. This factor α is the scale factor that is fully determined by the data. Using the effective density spectrum (e.g., Wieczorek et al., 2013), we interpret this factor as describing the bulk crustal density, if we choose x_a to be gravity from uncompensated topography (e.g., Wieczorek and Phillips, 1998).  In this way, we can estimate the bulk crustal density directly from the satellite tracking data. The constraint is described in detail in Goossens et al. (2017).

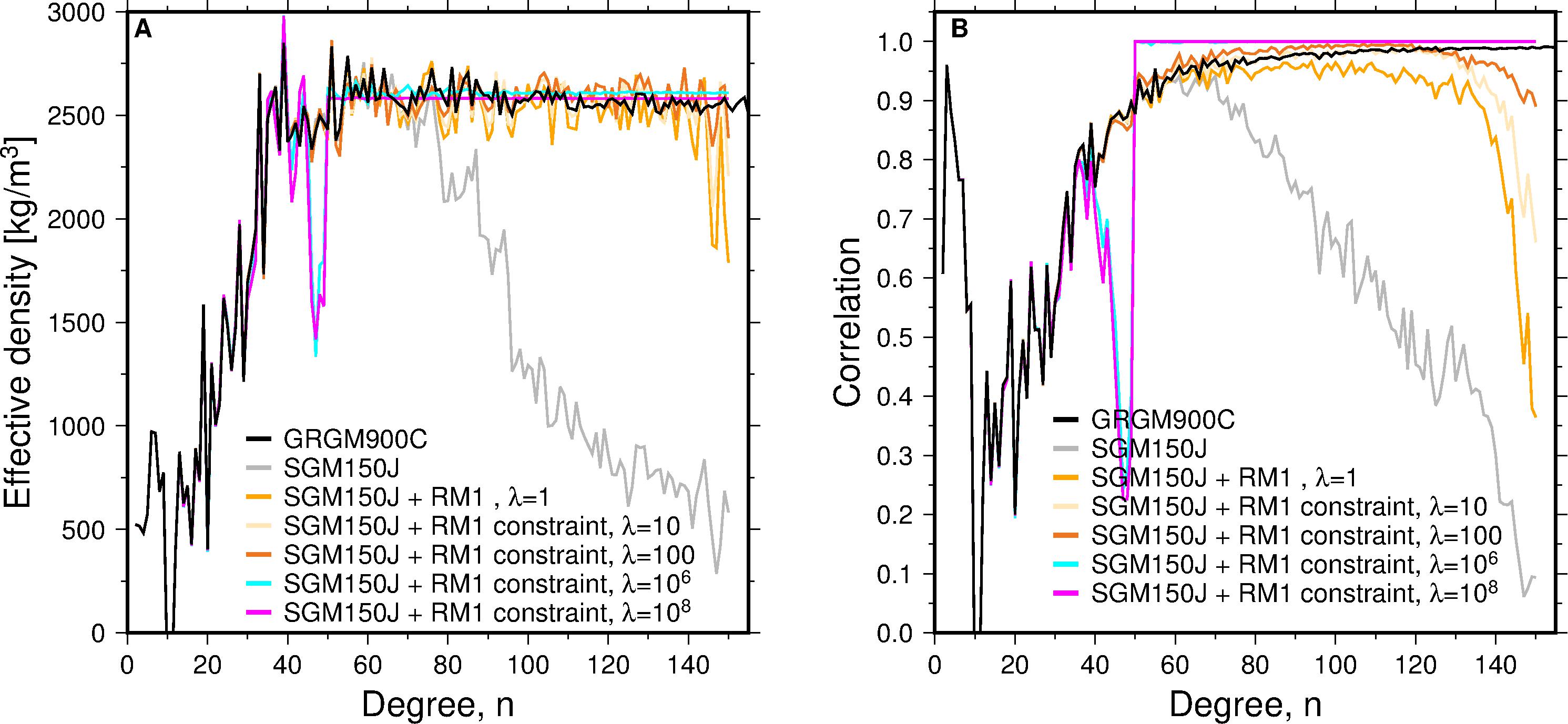
Figure 1. Effective density (A) and correlations between gravity and gravity-from-topography (B) for various models based on the SGM150J data matrix system. Our RM1 constraint model matches the results of the independent GRAIL model GRGM900C (Lemoine et al., 2014), showing that we can derive the crustal density robustly.

Using the data system of the pre-GRAIL lunar gravity model SGM150J (Goossens et al., 2011), we can robustly and independently determine the average bulk crustal density directly from the tracking data, using the admittance between topography and gravity: with the SGM150J data system and our RM1 constraint we find the same result as GRAIL. Thus, even for systems that are resolved not nearly as well as GRAIL’s, and therefore have an effective resolution well below the degree where the admittance becomes asymptotic (e.g., Wieczorek et al., 2013), we can still obtain a reliable estimate of the bulk density.

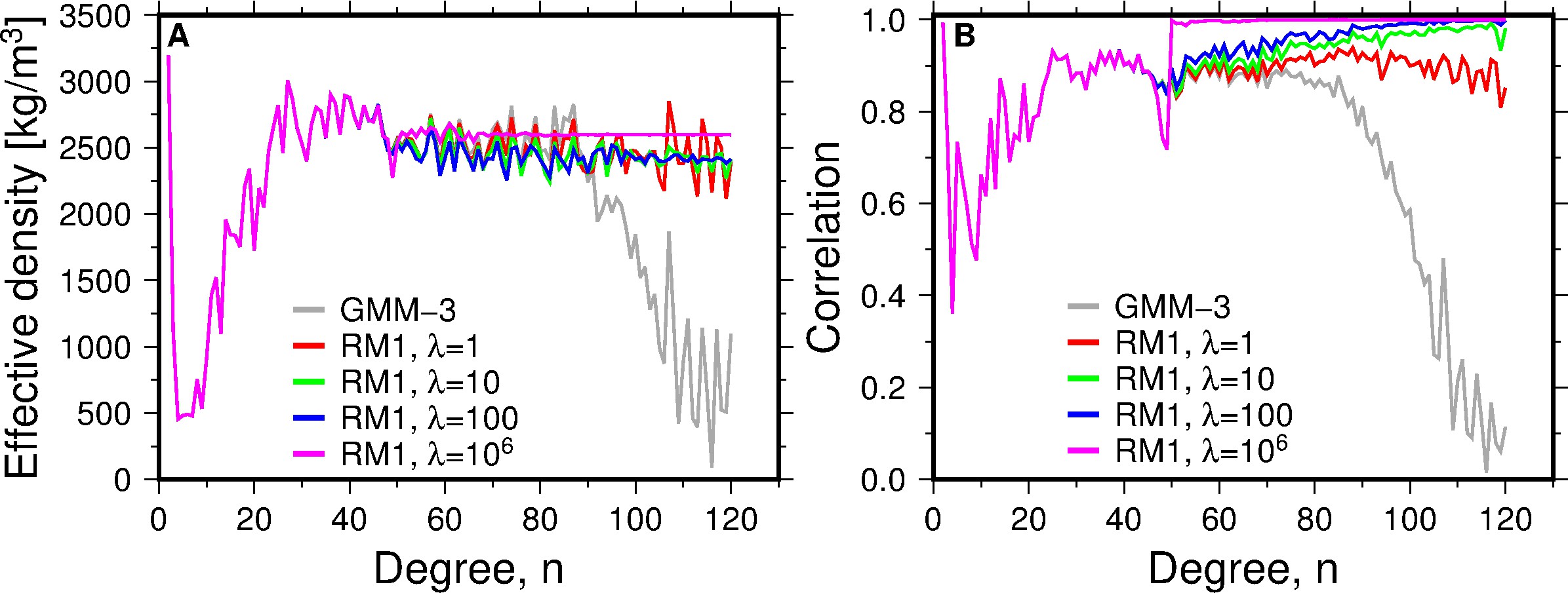
Figure 2.  Effective density (A) and correlations between gravity and gravity-from-topography (B) for various Mars gravity models. The RM1 constraint was applied with varying damping factors λ.

We have applied this constraint to gravity field determination using the data from Mars orbiters that were also used for the GMM-3 gravity field model (see Genova et al., 2016). We find a bulk crustal density for Mars of 2582 +/- 209 kg/m³, lower than generally assumed. The density for the volcanic complexes is higher: from our model we find a density for Pavonis of 3231 kg/m³, in good agreement with earlier estimates (e.g., Belleguic et al., 2005). The difference between the average density and the density for the volcanoes indicates strong lateral variations for Mars' crustal density. The lower bulk crustal density also has implications for models of the crustal thickness of Mars. The Mars results are further described in Goossens et al. (2017).

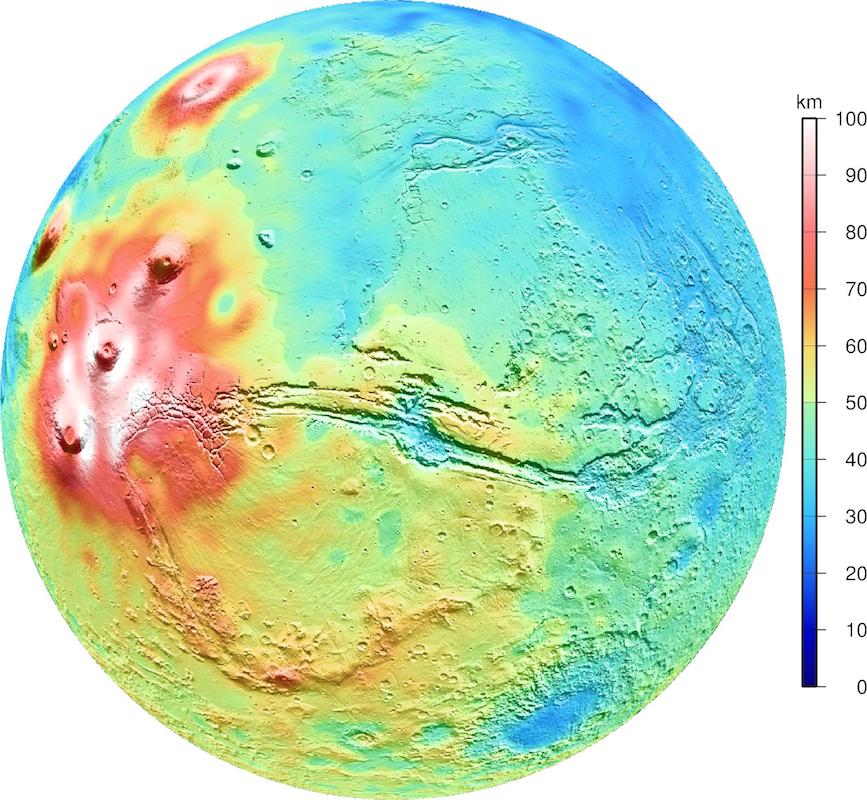
Figure 3. An example of Mars' crustal thickness using our lower crustal density (while applying a higher density of 2900 kg/m³ to volcanic complexes).

Data

The following data products are provided through this webpage (see Goossens et al. (2017) and Supplementary Information for more information on several of the products):

- Mars gravity models expressed in spherical harmonics of degree and order 120, based on the GMM-3 data matrix, derived with our RM1 constraint using various damping factors λ (see also Figure 2): links for λ=1, λ=10, λ=100, and λ=10⁶. See below for a description of the format of the files.

- Mars gravity model of degree and order 150, based on the GMM-3 data matrix, derived with our RM1 constraint with λ=1. [link]

- Our constructed density map for Mars (see also Fig. S15 in Goossens et al., 2017): a density of 2582 is used except in volcanic complexes where 2900 kg/m³ is used. This is a NetCDF GMT grid file. [link]

- This same constructed density in a spherical harmonic expansion of degree and order 149. The file format is the same as that of the Mars gravity models. [link]

- A map of example of how density may vary laterally on Mars, constructed through localization using our GMM-3 RM1 model with maximum degree and order of 150. We used a cap radius of 20°, L_win=20, and 30 tapers. We averaged the resulting localized effective density spectra between degrees 50 and 85. This is a NetCDF GMT grid file. [link]

- A map of localized correlations between gravity and gravity-from-topography using our GMM-3 RM1 model with maximum degree and order of 150. We used a cap radius of 20°, L_win=20, and 30 tapers. We averaged the resulting correlation spectra between degrees 50 and 85. This is a NetCDF GMT grid file. [link]

- A map of crustal thickness using our constructed density map. This is a NetCDF GMT grid file. [link]

Format of the spherical harmonic files:
These data files are ASCII files. The header for gravity files contains the gravitational constant GM (m³/s²), the mean radius a_e (m), and the maximum degree and order. For the density file the values in the location for GM and a_e are set to 1. The rest of the files contain lines with values for "order, degree, C_n,m, S_n,m". The C_n,m and S_n,m coefficients are the normal geodesy 4π normalized coefficients.

Data Usage Policy

Please cite the following reference when using any of the products described above:

Goossens, S., Sabaka, T.J., Genova, A., Mazarico, E., Nicholas, J.B., Neumann, G.A. (2017), Evidence for a Low Bulk Crustal Density for Mars from Gravity and Topography, Geophysical Research Letters, doi:10.1002/2017GL074172.

References

Belleguic, V., Lognonné, P., and Wieczorek, M. (2005), Constraints on the Martian lithosphere from gravity and topography data, Journal of Geophysical Research: Planets, 110(E11), E11005, doi:10.1029/2005JE002437.

Genova, A., Goossens, S., Lemoine, F. G., Mazarico, E., Neumann, G. A., Smith, D. E., & Zuber, M. T. (2016). Seasonal and static gravity field of Mars from MGS, Mars Odyssey and MRO radio science. Icarus, 272, 228-245.  doi:10.1016/2016.02.050

Goossens, S., Matsumoto, K., Liu, Q., Kikuchi, F., Hanada, H., Lemoine, F.G, Rowlands, D.D., Ishihara, Y., Noda, H., Namiki, N., Iwata, T., and Sasaki, S. (2011), Improved high-resolution lunar gravity field model from SELENE and historical tracking data, in American Geophysical Union Fall Meeting, abstract P44B-05.

Goossens, S., Sabaka, T.J., Genova, A., Mazarico, E., Nicholas, J.B., Neumann, G.A. (2017), Evidence for a Low Bulk Crustal Density for Mars from Gravity and Topography, accepted at Geophysical Research Letters.

Lemoine, F. G., Goossens, S., Sabaka, T.J., Nicholas, J.B., Mazarico, E., Rowlands, D.D., Loomis, B.D., Chinn, D.S., Neumann, G.A., Smith, D.E., and Zuber, M.T. (2014), GRGM900C: A degree-900 lunar gravity model from GRAIL primary and extended mission data, Geophysical Research Letters, 41(10), 3382–3389, doi:10.1002/2014GL060027.

Wieczorek, M. A., and R. J. Phillips (1998), Potential anomalies on a sphere: Applications to the thickness of the lunar crust, J. Geophys. Res., 103(E1), 1715–1724, doi:10.1029/97JE03136

Wieczorek, M. A., Neumann, G.A., Nimmo, F., Kiefer, W.S., Taylor, G.J., Melosh, H.J., Phillips, R.J., Solomon, S.C., Andrews-Hanna, J.C., Asmar, S.W., Konopliv, A.S., Lemoine, F.G., Smith, D.E., Watkins, M.M., Williams, J.G., and Zuber, M.T., (2013), The Crust of the Moon as Seen by GRAIL, Science, 339(6120), 671–675, doi:10.1126/science.1231530.

Product Keywords