NASA’s Planetary Geology, Geophysics and Geochemistry Laboratory

Patched Local Lunar Gravity Solutions using GRAIL Data

We present a new lunar gravity field model which is the product of a localized analysis of data from the Gravity Recovery and Interior Laboratory (GRAIL) mission (Zuber et al., 2013). We based our analysis on our earlier work where we employed the sensitivity of GRAIL’s inter-satellite Ka-band range-rate (KBRR) data with respect to small-scale features to determine a local model for the Moon’s south pole area (see here, and Goossens et al., 2014). Now, we extend this to the entire Moon. We divided the Moon into 14 overlapping regions, and for each region we determined a gravity field solution using KBRR data, processing the data over short periods of time (arcs; typically they were 25 minutes long). This is based on the approach of Rowlands et al. (2002). We express gravity as gridded gravity anomalies that are additional to a background global model in spherical harmonics. This background global model was the GRGM1200A model (see here, and Goossens et al., 2016; 2020). The gravity anomalies have a resolution of 0.15° by 0.15°, which is equivalent to a model in spherical harmonics of degree and order 1200. We apply neighbor smoothing following Rowlands et al. (2010) and Sabaka et al. (2010). For each area, we determine an optimal smoothing factor, by comparing localized correlations with topography for each solution, and by selecting the solution (and accompanying smoothing factor) with the best correlations. We show the areas and the optimal smoothing factors we selected in Figure 1. We iterated each local solution twice.


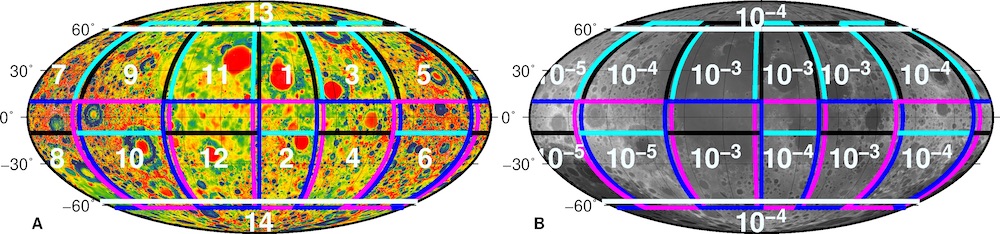
Figure 1: The 14 areas for which we determined local solutions (left, A), and the smoothing constraint factors that we applied (right, B). The projection is a Mollweide projection centered on the nearside.

We then patch the solutions into one global map by leaving out 5° at the edges to account for boundary effects. The patched solution (shown in Figure 2) shows no seams. We express the new model in spherical harmonics through spherical harmonic transformations. The resulting model has a maximum degree and order of 1199 (the grid spacing for the transformation uses N_max+1, and hence we use N_max = 1199 for a regular spacing of 0.15°). When we compute global and local correlations with topography (Figure 3), this new patched model has improved correlations compared to the start model GRGM1200A, and also compared to a full iteration of this model, GRGM1200B (see here, and Goossens et al., 2020).


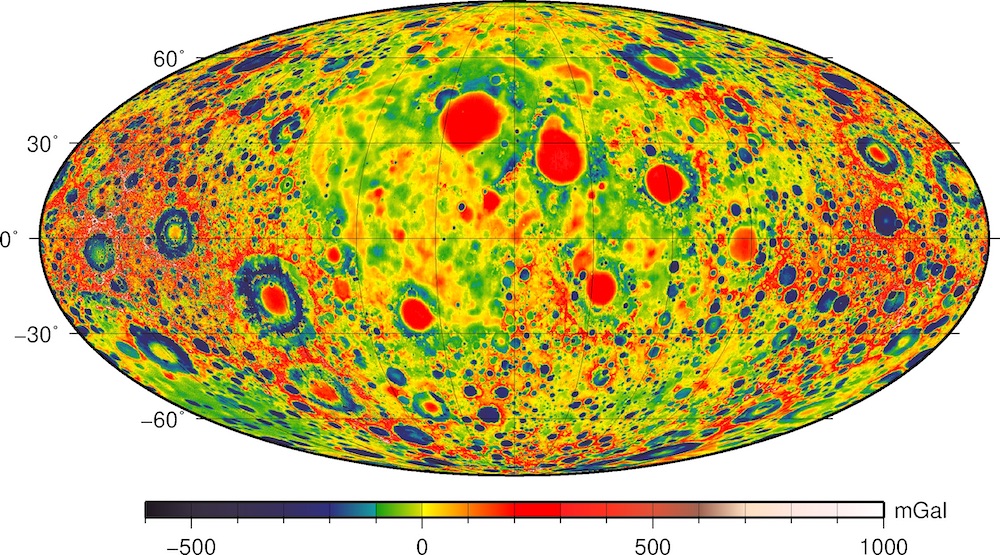
Figure 2: The global map of lunar gravity from our local solutions, at its full resolution of 0.15° by 0.15°. The projection is the same as in Figure 1.


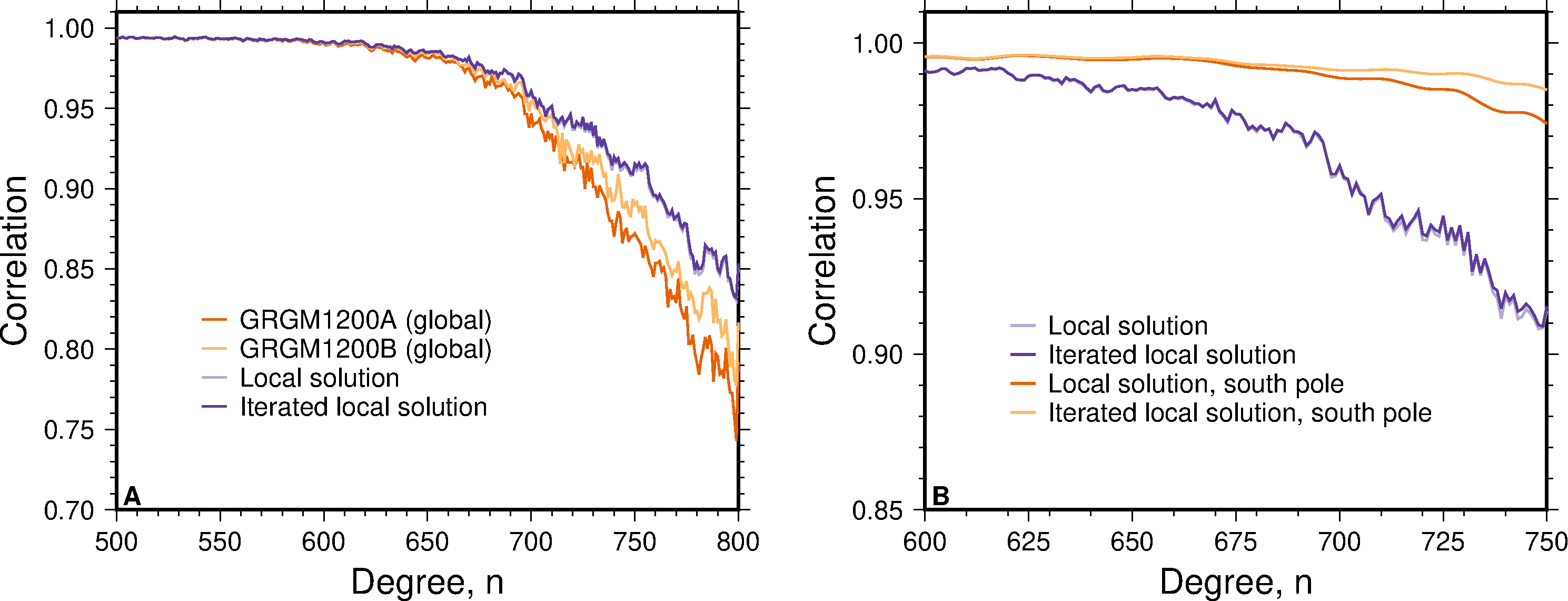
Figure 3: Global correlations between gravity and topography for the start model GRGM1200A, the fully iterated global model GRGM1200B, and our local solutions (both iterations) (left, A), and a close-up of only the local models that also includes correlations localized over the south pole (right, B).

The local model can be used at its full resolution of 0.15° by 0.15°: when we inspect a local area such as Mare Orientale (shown in Figure 4), we hardly see stripes in the anomaly map, as opposed to inspecting a global model at its full resolution. This is because we applied the neighbor smoothing to the entire signal. Localized correlations (Figures 3 and 4) also show improvements for the local model, which indicates that the smoothing clearly improves the solution, and results in a substantial increase in resolution. For example, our Mare Orientale solution crosses correlations with topography of 0.9 at a (localized) degree of 764 whereas the start model does this at the lower value of 725.


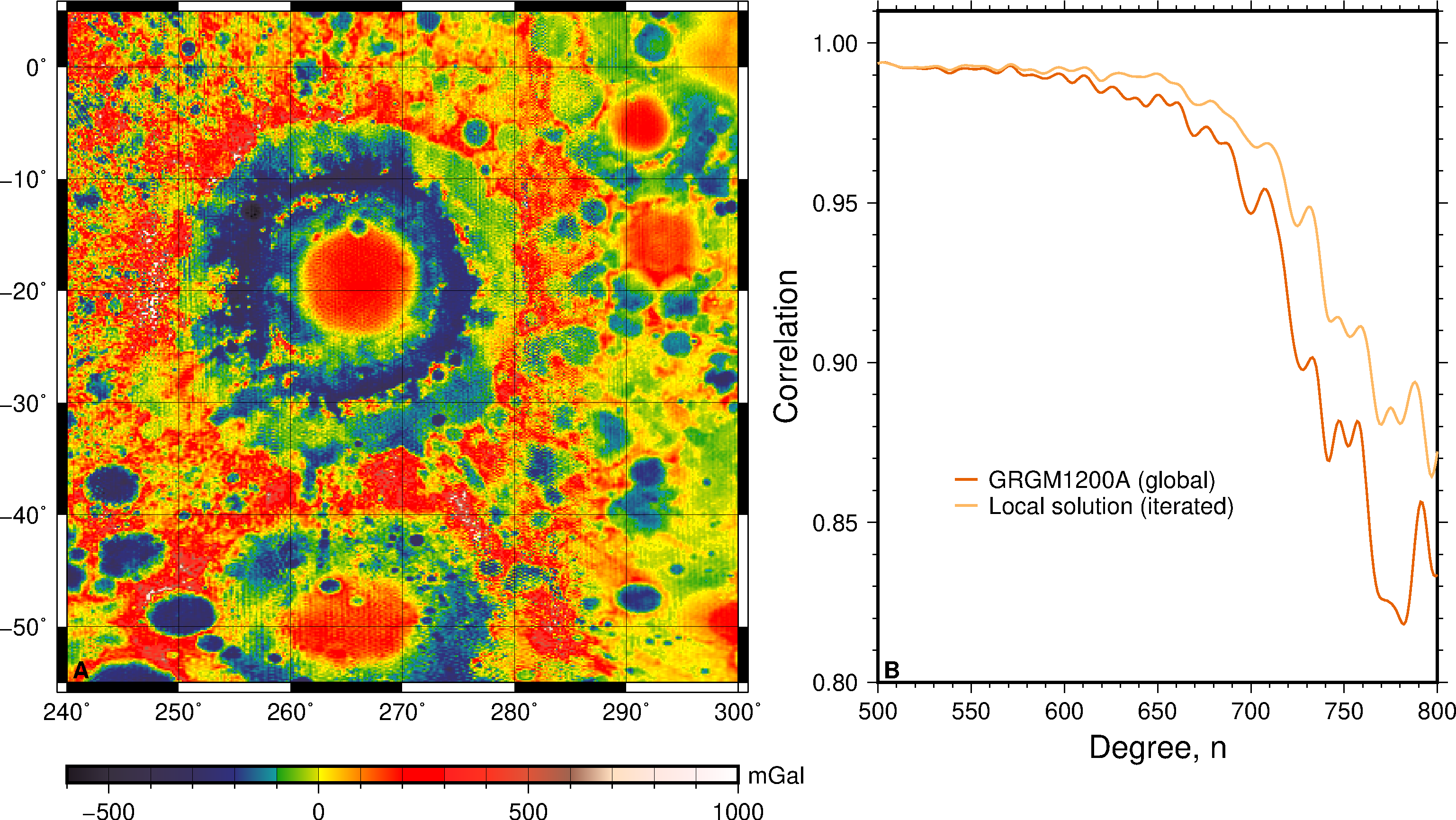
Figure 4: The local solution for Mare Orientale, at its full resolution of0.15° by 0.15° (left, A), and localized correlations with topography for the start model and local model (right, B).

Our local solution shows a mostly smooth and clear gravity signal, delineating feature boundaries clearly and with less noise than a global model at the same resolution would. The local model can be used in detailed analyses of the lunar crust. We do stress that spectral analysis of the local solution should still be undertaken with care, as correlations with topography show decreasing values with increasing degree.

This local approach is versatile in that the constraints can easily be varied regionally (Figure 1). In addition, this local approach requires fewer computational resources, and it can thus be an alternative to a global approach.

Here, we provide the spherical harmonic coefficients of the local model that we call GRGM1200L, as well as additional data sets, such as the spherical harmonics of the Bouguer expansion (using the algorithm of Wieczorek and Philips (1998), raising topography to the 20th power and using a constant crustal density of 2550 kg/m³), and NetCDF grid files for the free-air anomaly, and Bouguer disturbances at two different maximum degrees. For the maps of free-air and Bouguer gravity, we also include GeoTIFF images.

Data

Data Usage Policy

References

Product Keywords